Главная  Теория  Логика принятия решений в современном бизнесе

Некоторые аспекты ранней диагностики / контроля (методология ГЛАС^®)

Соколюк В. Н.

Настоящая работа профессиональна и представлена для аргументированной критики, без скидок на недостаточные знания. Данная методология применима к любым событиям, субъектам, объектам (техническим, социально-экономическим). Ограничение по точности ограничено только техническим прогрессом фиксирующих датчиков.

Введение

В настоящей работе предлагается новый метод диагностирования, построенный на математическом аппарате непрерывнозначной логики [1].

Общеизвестно, что внезапные отказы наступают реже постепенных. Так, по некоторым литературным источникам, соотношение постепенных и внезапных отказов порядка 100:1 [2, стр.269]. Это говорит о том, что работающая сложная система не дает сбоя, но ее параметры могут отклоняться от предусмотренных нормативных показателей. Понятно, что эти отклонения от нормы различных элементов сложной системы не могут не сказываться на работоспособности всей системы в целом. Поэтому возникает насущная потребность в оценке состояния сложных систем для того, чтобы произвести вовремя все необходимые мероприятия и тем самым предупредить сбой системы. Это особенно актуально для быстрых и плохо формализуемых процессов (особенно социальных). Авторы хотят предложить настоящую методологию для оценки состояния социально-финансовых институтов, в частности бюджетных институтов, банков. Мы сразу хотим сообщить уважаемому читателю, что система настолько сложна, что аналитически выразить связь между отдельными параметрами системы практически невозможно, а тот, кто утверждает обратное, очень и очень заблуждается...

Поэтому основной посылкой в данной методологии является учет структурно-логических связей рассматриваемой сложной системы, так как это позволяет оценивать динамику поведения этой системы, осуществлять непрерывный контроль (мониторинг) за всеми параметрами, проводить анализ и имитировать различные состояния. Данная методология была создана в 1987 году [3, стр.75].. Мы также хотим заметить, что в это время активно разрабатывались стандарты и методологии структурно-логического анализа, информационно-логического анализа, а также различные программные продукты, поддерживающие технологии структурного анализа (SADT, система стандартов IDEF…). Данные технологии активно используются для проведения реинжиниринга и активно применяются практически всеми компаниями, которым не безразлично свое будущее [4].

Замечание. Предлагаемый ниже метод не заменяет собой метод допускового диагностирования, иногда его называют метод нормативного контроля (контроль за нормативами). Данный метод также не заменяет и метод контроля по показателю качества. Из самой формулировки задачи будет видно, что предлагаемый подход к диагностированию сложных систем разительно отличается от тех, которые существуют в настоящее время. По нашему глубокому убеждению, он (метод ГЛАСТМ) объединяет все существующие методы, а может даже и поглощает их.

Метод относится к универсальным, ориентированным на любые объекты диагностирования, для которых тем или иным способом описана их логическая структура. Из методов, ранее описанных в литературе, предлагаемый относится к методу контроля по показателю качества, хотя также имеет много общего и с методом функционального контроля (непрерывного контроля за функциями). Автору думается, что данный метод охватывает уже известные методы, добавляя и формализуя логические и качественные связи. Общность и различия будут видны более весомо по ходу изложения настоящего материала.

Уточним отправные пункты всех наших построений:

• состояние любой системы в целом в любой момент времени характеризуется некоторым числом, которое зависит как от состояния элементов системы, так и от логических (причинно-следственных) связей между ними;
• у каждого элемента системы может быть бесконечно много состояний, каждое из которых оценивается некоторым числом;
• состояния элементов системы четко не различимы, они расплывчаты, имеют некоторый интервал.

Постановка задачи

Допустим, что известна логическая модель сложной системы, например информационно-логическая (инфологическая), состоящая из n-элементов, а качественная работа каждого элемента этой системы пусть оценивается по некоторой непрерывной шкале (можно даже и субъективно, например методом экспертных оценок). Требуется оценить (то есть поставить сложной системе в соответствие число) качество работы всей системы в целом с учетом оценок элементов и их связей между собой.

Алгоритм решения задачи

1. Располагая структурной принципиальной или иной схемой объекта диагностирования, строим его функциональную модель. Вопрос об оптимальности деления системы на блоки представляет собой самостоятельную задачу, решение которой не является целью настоящей работы. Критерий оптимальности должен включать в себя, по-видимому, такие показатели, как:

• удобство представления входных и выходных параметров блока;
• локализация функций и их взаимоувязка;
• удобство измерения входных и выходных параметров блока и т.д.

2. По функциональной модели строим логическую модель. Однако будем считать, что все обратные связи в рассматриваемом объекте на время диагностирования разрываются (например, заменой группы блоков, охваченных обратной связью, одним эквивалентным им блоком). Таким образом, логическая модель, соответствующая рассматриваемому объекту, будет без обратных связей.
3. Далее, по логической модели строим граф, заменяя блоки логической модели вершинами графа, а связи между блоками — ребрами. Получим направленный граф без контуров и петель. На множестве вершин такого графа определим отношение порядка следующим образом: присвоим вершинам графа такие номера, чтобы каждое направленное ребро выходило из вершины с меньшим номером и входило в вершину с большим номером. Рассматриваем графы с одним входом и с одним выходом, однако это ограничение нисколько не уменьшает общности, поскольку всякий упорядоченный граф может быть приведен к такому виду. Это достигается добавлением двух фиктивных вершин: входной и выходной [5].

Очевидно, что в упорядоченном графе с одним входом и одним выходом существует конечное число путей из входной вершины в выходную. Эти пути можно упорядочить — пронумеровать.

Однако упорядочивание вершин графа с добавлением фиктивных вершин или без них можно и не проводить. Это облегчит построение теории и модели, если в этом есть необходимость, для применения различных методов и всесторонней диагностики сложных систем.

Для дальнейшего изложения метода ГЛАС^® введем некоторые понятия, определения и обозначения состояния сложной системы, т.е. будем говорить о ”качественной” и ”некачественной” работе системы (можно говорить о ”работоспособности” и ”неработоспособности” сложной системы), а, оценивая техническое состояние элементов системы, можно говорить о ”дефектности” и ”бездефектности” элементов системы или блоков системы. Однако мы будем говорить о качестве работы отдельных элементов системы, нам кажется, это больше соответствует здравому смыслу. Причем качество мы будем понимать в самом широком смысле этого слова.

Итак, объекты рассмотрения — это сложные системы, с которыми отождествляются или функциональные модели, или их блоки (т.е. элементы системы), формализованные посредством графа. Если объект рассмотрения — А, то через Н[А] — обозначим значение оценочного функционала, т.е. число, которое ставится в соответствие объекту А. В дальнейшем оценочный функционал будем истолковывать как работоспособность, бездефектность, исправность. Однако мы помним, что желательно работать в терминах «качественно — некачественно», «хорошо — плохо» и просим читателя набраться терпения, т.к. эти термины пока еще у нас не определены, а именно, не определен порядок вычисления и формализации значения «качество».

О качестве мы обязательно поговорим несколько позже. А сейчас мы будем говорить о работоспособности, т.е. в понимании двузначности «работает — не работает», это будет полезно для усвоения методики и только. Причем, мы прекрасно понимаем, что значения порогов (работает – не работает) у различных субъектов разное, но это допущение, как видно будет из дальнейшего изложения, не влияет на метод. Это может влиять только на точность модели, на ее адекватность реальной действительности, но это не является целью настоящей работы, т.к. постановкой и формализацией модели занимаются специалисты предметной области, желающие применить данную методику. Мы предлагаем только оценочный математический аппарат.

Итак, объект рассмотрения, противоположный объекту А, будем обозначать как aА, а оценки соответственно H[A] и H[αA]. Объект А полностью бездефектен и мы его будем выражать, как H[αA] = 0, или H[A] = ∞ и, наоборот, при абсолютной дефектности H[αA] = ∞или H[A] = 0. Далее будем различать системы двух видов, которые отличаются своими свойствами и имеют следующие определения.

Краткое описание формального аппарата

Определение 1.
Будем говорить, что элементы сложной системы A и B имеют между собой β- связь (т.е. AβB ), если выполняются следующие условия;
1. Система тем работоспособней, чем бездефектнее ее элементы;
2. Система полностью работоспособна, если абсолютно бездефектен хотя бы один элемент сложной системы;
3. Система полностью неработоспособна, если полностью дефектны все ее элементы.
И в случае независимости элементов A и B будем вычислять связку AβB, согласно равенству

Анализируя выражение (1), видим, что оно полностью отвечает условиям определения 1. Таким образом, равенство (1) моделирует определение системы AβB .

Однако обращаем внимание читателя на существенность и естественность первого пункта определения 1. Он фиксирует кажущуюся очевидным зависимость оценки состояния сложной системы от всех ее элементов, а не от одного или нескольких элементов системы, выделенных по тому или иному признаку из множества всех элементов сложной системы. Как будет показано далее, это свойство системы или систем в полной мере не может быть выражено средствами логики Л.Заде (нечеткие множества).

Теперь обратимся к системам другого вида и начнем с их определения..

Определение 2.
Будем говорить, что элементы A и B имеют y-связь (т.е. AyB), если выполняются следующие условия:

1. Система тем работоспособнее, чем бездефектнее ее элементы;
2. Система полностью работоспособна, если абсолютно бездефектны все ее элементы;
3. Система полностью неработоспособна, если хотя бы один ее элемент полностью дефектен.
И система AgB в случае независимости друг от друга элементов A и B будет вычисляться, согласно равенству

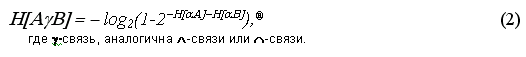
Анализируя выражение (2), замечаем, что оно полностью соответствует условиям определения 2, а роль пункта 1 столь же существенна, как и в определении 1, таким образом, выражение (2) определяет системуH[AyB]..

Изложенные определения 1 и 2 легко могут быть распространены на системы, состоящие из n-элементов. Таким образом, если мы имеем n-элементов А1, А2, ... Аn и эти элементы независимы в совокупности [1] имеем:

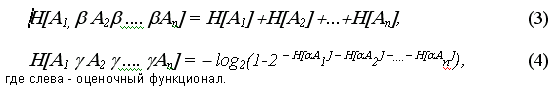
Заметим, что предлагаемый метод позволяет формализовывать и рассматривать системы, которые состоят из зависимых элементов. Однако мы сознательно не будем рассматривать этот случай, поскольку он связан с усложнением только технической стороны вопроса без изменения принципиальной сути. Если у кого-то возникнет желание работать с зависимыми элементами, то есть при различных условиях, могут обратиться к имеющимся публикациям [1,6,7].

Итак, вооружившись нужными определениями и обозначениями, продолжим описание принципиальной схемы решения, сформулированной ранее нами задачи.

4. Допустим, что в момент проверки состояния сложной системы известны степени дефектности (или бездефектности) всех ее блоков в отдельности, на которые она распалась при составлении функциональной модели. Будем считать, что бездефектность блоков оценивается по какой-то непрерывной шкале. Однако мы хотим сразу предупредить читателя, что нами в данной работе подходы к выбору шкал даже не рассматриваются. Этим занимаются теория шкал, многомерная геометрия и другие родственные науки, которые достаточно хорошо изучены и апробированы на практике, поэтому авторы не будут останавливаться на этом вопросе, хотя выбор шкалы — очень ответственный момент.

Итак, каждой вершине упорядоченного графа с одним входом и одним выходом поставлено в соответствие число (назовем его некоторое число, т.к. мы не определили шкалы), таким образом, мы имеем таблицу, которую назовем оценочной:

5. Зная оценочную таблицу для упорядоченного графа с одним входом и одним выходом, мы всегда сможем построить матрицу дефектности путей, т.е. диагностическую матрицу, где вверху указаны номера вершин графа, а справа — номера путей, а на пересечении i-ой строки и j-го столбца стоит степень дефектности j-го блока. В матрице А* (как пример, Рис..1) в i-ой строке ставится степени дефектности блоков, принадлежащих i-му пути, а если j-ая вершина не принадлежит i-му пути, то на пересечении i-ой строки и j-го столбца можно поставить ноль, таким образом мы можем иметь матрицу размерности {n•m} и любой степени “вложенности”, т.е. каждое значение матрицы может быть раскрыто в матрицу произвольной размерности и т.д. (автор решал размерности {400•400} с вложенностью 400, то есть [{400 •400}•400].

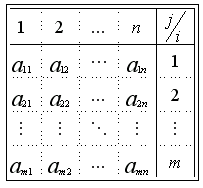
Рис. 1. Матрица А*

6. Может оказаться, что блоки в функциональной модели не все равноправны, тогда им мы будем приписывать весовые коэффициенты r1, ....rn (суррогат зависимых связей). Здесь n-число блоков. Таким образом, может оказаться, что в вершине графа приписаны и степень дефектности соответствующего блока и весовой коэффициент. В аналогичном положении находятся и пути в графе. Коэффициент, который соответствует i-му пути в графе, обозначим посредством ri. Итак, мы имеем упорядоченный граф с одним входом и одним выходом, вершинам которого поставлены в соответствие некоторые числа. Очевидно, что между графами рассматриваемого вида и матрицей путей всегда существует взаимно однозначное соответствие. Напомним, что граф был связан однозначным соответствием с логической моделью, а через нее и с функциональной моделью. А потому матрицу можно рассматривать в качестве модели объекта диагностирования. Теперь для получения общей оценки работоспособности необходимо дать алгоритм, который бы позволил любой матрице поставить в соответствие некоторое число.

7. Решение задачи

Сначала рассмотрим определение “блок”. Допустим, что мы имеем объект диагностирования с резервными блоками. Таким образом, слово “блок” в данном случае мы понимаем как некоторое сложное обобщение между блоками, которые ранее мы считали неделимыми и входящие в систему как нечто целое. Теперь же под “резервным блоком” будем понимать нечто такое, что может быть заменено чем-то равносильным, может дубликатом, который состоит из нескольких прежних блоков. Чтобы не было путаницы, будем говорить о блоках и квазиблоках, т.е. о составных объединенных блоках. Учитывая связь между функциональной моделью и матрицей путей, заключаем, что все связи внутри объекта диагностирования можно разбить на две группы:
· связи между резервными квазиблоками;
· связи между блоками внутри резервных квазиблоков (это то, что мы ранее называли вложенностью). Определим это как многоуровневый системный подход.

А теперь вспомним определение 1 и 2 в части связей, которые символизируются знаками β и y, откуда видно, что резервные квазиблоки связаны между собой знаком y, а блоки внутри них связаны знаком β. Резервному квазиблоку в целом соответствует некоторый путь в графе (строка в матрице путей). Таким образом, i-му пути (в i-ой строке) ставится в соответствие следующие числа

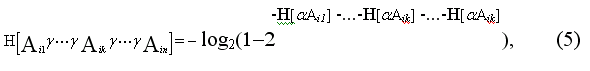
где К(1≤K≤n) — номер узла в графе;
n - общее число узлов в графе;
H[αAik] — степень дефектности К-го блока.
Используя оценочную таблицу, получим:

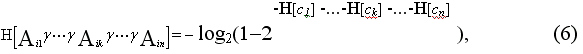
где Сk = ak , если К-ый узел принадлежит i-му пути, и Сk =0, если К-ый узел не принадлежит i-му пути.

Всей же системе (графу, матрице) ставится в соответствие число:

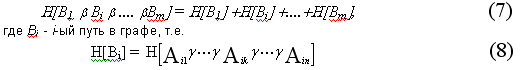
Таким образом, упорядоченному графу с одним входом и одним выходом (матрице путей) можно поставить в соответствие число, вычисляемое по формуле (7). В случае рассмотрения технической системы без резервных квазиблоков, с неравноправием как блоков так и их объединений, вычисления следует вести согласно равенствам:

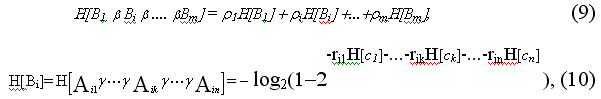
Замечания: Оценивая состояние той или иной системы, пользуются разными шкалами [8,9] при оценке состояний разных элементов системы. Введение весовых коэффициентов rik и ri (суррогат учета зависимости элементов системы), где

 
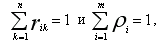
с нужными индексами дает возможность формализовать этот процесс, происходящий в сознании человека, скорее всего на уровне интуиции. Правильность выбора шкал отражает опыт эксперта, оценивающего состояние системы. В самой упрощенной форме можно смоделировать процесс диагностирования, который бы удовлетворял различным критериям.
Например, мы можем оценивать состояние сложной системы даже по одному элементу, когда необходимо выяснить роль К-го блока. В этом случае rk =1, ri=0 (i=1,...,n; i≠k). В качестве такого “единственного” элемента может фигурировать элемент, имеющий минимальную или максимальную оценку работоспособности или среди всех элементов системы, или среди части элементов системы. Если же оценивать состояние сложной системы по нескольким элементам, то этот случай представляет собой обобщение предыдущего случая. Им пользуются, например, когда не хотят учитывать состояние всех элементов системы, а учитывают только состояние наиболее важных с какой-то точки зрения объектов диагностирования. Такой подход сродни методу линеаризации, однако по нашему мнению все-таки необходимо упрощать тогда и только тогда, когда есть знания о более сложной модели и она всесторонне изучена, т.к. зачастую можно не уловить малые, но очень существенные блоки (квазиблоки) или функции (подфункции) сложной системы и получить не адекватную практике (жизни) модель.

Сравнение различных методов

Остановимся теперь на сравнении представленной методики с существующими современными теориями, например с теорией нечетких множеств, разработанной Лютфи Заде (нечеткие логики). Сначала отметим, что справедливо неравенство [3,6,7]:

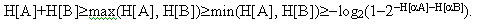
Отсюда следует, что в случае независимости А и В друг от друга имеет место неравенство

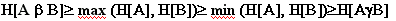
Иными словами, вычисление коньюнкции и дизъюнкции средствами логики Л.Заде дает результаты, заключенные между H[AyB] и H[AβB]. Таким образом, оценки по теории нечетких множеств представляют собой частный случай оценок состояния сложных систем, согласно построенной ранее модели.

Продемонстрируем “несовершенство” логики Заде. Очевидно, что состояние сложной системы (а значит и ее оценка) зависит от всех элементов системы. Такое понимание вещей нашло отражение в первых пунктах определений 1 и 2. Отмеченное свойство не “улавливает” логика Заде. Действительно, пусть H[A1]=1, а H[В]=0,3, тогда согласно логике Л.Заде имеем

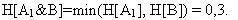
Пусть теперь Н[A2] = H[B] = 0,3. И в этом случае Н[A2&B]=min(H[A2], H[B]) = 0,3, хотя вряд ли любой здравомыслящий человек согласится с тем, что замена абсолютно бездефектного по Заде блока (.H[A1]=1) на дефектный Н[A2] = 0,3 не отразится на всей системе в целом. А описанный в данной работе метод “отреагирует” на изменившуюся обстановку (состояние) сложной системы. Действительно, имеет место неравенство

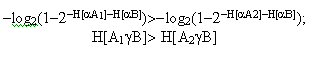
Таким образом, чем меньше исправность, работоспособность, качество (т.е. больше дефектность) элементов сложной системы, тем меньше работоспособность всей системы в целом.

Выводы

Описанная методика позволяет точнее улавливать и анализировать (моделировать) сложные системы (процессы), что весьма полезно в реальном деле [8,9].

Также мы хотим отметить, что прежние методы оценивали работоспособность (качество) системы через работоспособность (качество) отдельных блоков без всякого учета связей (логических связей), а это на наш взгляд весьма далеко от жизни. То есть логические связи между блоками ранее использовались не для отыскания плохо работающего блока, а для отыскания отказавшего блока, т.е. когда уже факт (отказ) произошел и его можно только заменить, но ведь в жизни в любом реальном коллективе так никогда не бывает. Да и сама система, сколь сложна она не была, мыслилась разбитой на блоки, каждый из которых как бы находился в отдельном ящике на стеллаже склада; ящики можно переставлять, ничего при этом не меняя, поскольку общая оценка определяется состоянием одного или нескольких блоков, без какого-либо учета связей между ними. Этот постулат очень сильно отражает стиль управления многих руководителей и объясняет крылатую фразу «хотим как лучше — получается как всегда», но мы должны сразу предупредить, что такое понимание вещей ведет к ошибке в ~70%, что можно строго доказать.

В предлагаемом же методе существенна связь между блоками, она влияет на общую оценку. При таком подходе к оценке состояния системы есть возможность, если известна логическая структура системы, определить, какой должна быть работоспособность отдельных блоков, чтобы была работоспособна вся система в целом. Таким образом, новый метод позволяет решать не только задачу синтеза работоспособность системы по работоспособности блоков, но и задачу анализа, какая должна быть работоспособность отдельных блоков, если задана работоспособность всей системы в целом. Предложенные другими авторами методы диагностирования такой возможности не представляют. Также хотим отметить, что способы вычисления работоспособности отдельных блоков нами никак не регламентируются (полная свобода действий).

Задача о качестве (субъекта/-ов, объекта/-ов)
А теперь, уважаемый читатель, мы напомним Вам, что мы никак не определили термин «качество» или «качественная работа», а также как его или ее вычислять. Если у Вас еще осталось терпение нас правильно воспринимать, то мы постараемся в той же методологии формализовать этот процесс. Таким образом, мы попробуем вместе с Вами, уважаемый читатель, формализовать оценку качества, причем качество — его оценка (т.е. это понятие) может решаться во всем многообразии диалектического развития.

Понятие “качество” в общепринятой швейцарской терминологии стандартов определяется как “степень соответствия характеристик продукции предварительно установленным требованиям, включая такие из них, как надежность, удобство, безопасность обслуживания” [10].. Однако такой подход отражает главным образом точку зрения продуцента, между тем как потребителя интересует прежде всего пригодность продукта к использованию. Точки зрения потребителя и продуцента могут либо совпадать (полностью или частично), либо коренным образом различаться. И именно подход к качеству с точки зрения потребителя, по мнению многих исследователей (Д. Джуран и др.), является основной характеристикой качества, хотя и он не для всех случаев абсолютно правилен.

Все понятия качества (Ф.Никсона, А.Робертсона, Сакато-Сиро и др.) делятся на два вида:

• как пригодность к употреблению
• как соответствие технологическим и прочим требованиям.

Однако необходимо сказать, что ни одно из определений “качество” не является универсальным. Одно из самых распространенных понятий “качество” следующее: “....совокупность характерных свойств, формы, внешнего вида и условий применения, которыми должны быть наделены товары или услуги для соответствия своему назначению ...”[11]. Иногда качеством называют совокупность характерных особенностей, формы, внешнего вида и условий эксплуатации, определяющих пригодность товаров. Элементы, составляющие качество, называются показателями качества, а численное их выражение — значением показателя качества [12, 13]. Мы будем понимать термин “качество” в самом широком смысле этого слова, не разделяя точки зрения только потребителя или только продуцента.

Итак, уважаемый читатель, теперь мы намерены рассмотреть схему (методику) нахождения качества, причем предмет качества никак не оговаривается: это может быть и качество знаний, и качество работы, и качество изображения, и качество подготовки специалистов, и качество труда, и качество окружающей среды, и т.д. и т.п. Мы исходим из того, что о качестве любого объекта или услуги судят по степени выполнения требований, предъявляемых к объекту. Например, к корыту не предъявляются требования согревать квартиру в холодную погоду, хотя в жизни могут возникать требования к предмету, не очень свойственные ему по основным функциям (все мы знаем, как использовались бритвенные лезвия для кипячения воды).

Итак, допустим, что к какому-то объекту или процессу предъявляются требования N1,....,Nn. Пусть требование Nj (j=1,...,n) состоит из условий Mij, где i — количество условий того или иного требования. Совершенно естественно, что требования и условия, из которого состоит требование, между собой неравнозначны, но мы это формализуем через весовые коэффициенты, rj — весовой коэффициент требований Nj , а посредством rij — весовой коэффициент условия Mij .

Уточним исходные положения:

• качество проявляется, только тогда, когда мы предъявляем определенные требования к объекту, т.е. качество проявляется в процессе предъявления требований;
• любое требование зависит от ряда условий или состоит из ряда условий;
• каждое требование и каждое условие имеют свой весовой коэффициент в исследуемом процессе.

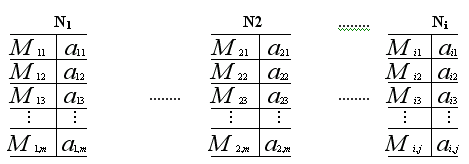
Таким образом, если требование — это параметр Ni, при i=(1,...n), а условия в каждом i-ом требовании — Mij, при j=(1,...m), то соответственно rj — весовой коэффициент требований Nj , а rij — весовой коэффициент условия Mij . Все эти параметры могут быть ранжированы существующими теориями в безразмерной шкале с некоторой долей субъективизма. В результате оценок всех перечисленных параметров, а точнее после выполнения всех условий и их оценок, получим таблицы, указанные выше.

Имея набор таких таблиц, попробуем получить число, характеризующее выполнение всех перечисленных требований. Заметим, что удовлетворить требованию Ni — это значит выполнить условия первое и второе, и третье и т.д., связка “И” говорит о логике наших действий, а удовлетворить всем требованиям Ni — значит удовлетворить объединению перечисленных требований Nn. Хотим сразу отметить, только что мы формализовали логику понятия “качества”, а раз так, то мы можем применить аппарат логики антонимов (непрерывнозначной логики). Задача вычисления степени выполнения всех требований и условий сводится к вычислению численного функционала

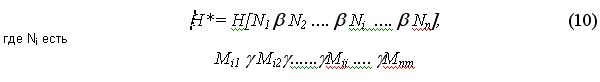
Выражение (10) необходимо понимать как некоторое неотрицательное число, которое ставится в соответствии объединению требований N1, .....Nn , а также как выражение, фиксирующее зависимости значений функционала Н* от его аргумента N1 b N2 .... b Ni .... b Nn

Для упрощения будем считать, что все -Ni независимы, тогда

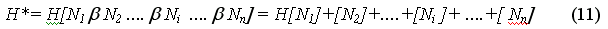
Здесь необходимо отметить, что математический аппарат непрерывнозначной логики применим и в случае, когда требования N1, .....Nn зависят друг от друга. Тогда формальная сторона изложения становится значительно сложнее, чем в рассматриваемом варианте (11), а суть дела не меняется, например для [Ni]

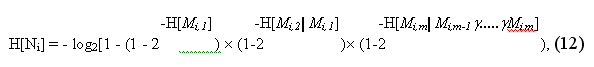
Поэтому будем считать, что требования не зависят друг от друга. А также и все условия не зависят друг от друга, тогда имеем:

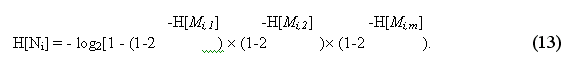
Однако если мы введем весовые коэффициенты, то можем получить некоторое приближение к реальности, а именно для выражения (11):

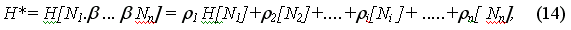
а выражение (13) соответственно

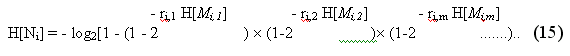
Теперь нам необходимо вспомнить, что у нас уже есть оценочные таблицы, где все наши оценки уже вычислены с учетом весовых коэффициентов, тогда мы имеем:

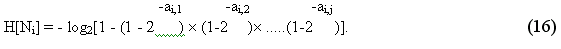
Итак, получив таблицы выполнения требований Ni , всегда возможно вычислить значение функционала Н*, характеризующее выполнение всех требований в совокупности — выражение (16).
Остановимся теперь на вопросе перевода оценки Н* в более привычную для нас форму «...что такое хорошо и что такое плохо ...». Легко заметить, что Н* является монотонно возрастающей функцией параметров H[Mi,j]. Если даже одно из значений H[Mi,j] равно нулю, то справедливо равенство H[Ni]=0.. Если все H[Mi,j] принимают максимальные значения, то и H[Ni]=max. Вычислим значение Н*, которое является максимальным из всех возможных значений. Это сделать возможно всегда, если известны верхние границы значений параметров H[Mi,j]. Далее укажем число К* такое, что в случае

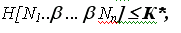
это является плохим показателем, а в случае, если

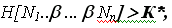
это является хорошим показателем. Указанное число К* является неким значением, которое отделяет область значений функционала Н*, при которых возможна хорошая оценка качества. Таким образом, число К* характеризует некоторую величину требовательности, и рассмотренная нами модель охватывает все сложные стороны формализации процесса качества не только со стороны продуцента, но и со стороны клиента (потребителя продукта). Это своего рода жесткая сцепка прав и обязанностей по любому вопросу качества (качество знаний, качество услуги, качество труда, качество управления и т.д., и т.п.).

По нашему глубокому убеждению, только такой подход отражает действительность и сущность вещей. Необходимо всегда помнить, что права и обязанности существуют как у продуцента, так и у клиента вне зависимости от его желаний. Так, например, если мы рассматриваем качество знаний, то число К* дает как право на выставление зачета, так и право на получения зачета.

Однако, описанная методология позволяет, по мнению авторов, сформулировать и другие подходы к оценке качества. Рассмотрим несколько вариантов.

1. “Ультратребовательный” подход к качеству, при котором невыполнение даже одного из условий Mi,j (H[Mi,j])=0 влечет неудовлетворительную оценку. Формально это можно выразить так: хорошо, если

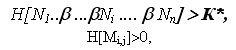
в противном случае считаем плохо.

2. “Ультраснисходительный” подход к качеству, при котором только невыполнение всех условий Мij приводит к итоговой оценке, равной нулю. Иначе, если

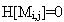
то это значит, что качество плохое, а во всех остальных случаях — хорошее.

3. “Требовательный” подход к знаниям, при котором невыполнение хотя бы одного требования приводит к некачественному понятию, т.е. формально хорошо, если

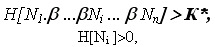
при других (противных) условиях — плохо.

Эти три примера можно формализовать и иначе, воспользуемся только логическими связками. Так, для первого примера достаточно в разрабатываемой модели (11) заменить знак β на знак y; для второго случая достаточно, чтобы в выражении (11) произошла замена знака y на знак β, а для третьего примера необходимо в выражении (11), все знаки β заменить на знаки y, а знаки y, заменить на знаки β.

Так вот, уважаемый читатель (потребитель или заказчик), этим абзацем мы показали, что изменение логики (логической связки) приводит к совершенно другому результату, в науке это называется софистикой (подменой понятий, заблуждением или просто незнанием логики процесса), “правда, это не освободит от ответственности”, и насколько это положение серьезно может влиять на принятие решений, мы Вам уже показали. Таким образом, во главу угла должен ставиться логический процесс деятельности (цели, функции...) их формализация, а не иные действия, и только потом эти или иные действия несколько могут (непротиворечиво) видоизменить основной процесс, но контролируемым и с прогнозируемыми последствиями образом.

Авторы не показали всего многообразия логических структур, используемых при оценках качества, но уважаемый читатель, наверно заметил, что мы указали как бы граничные варианты, и остановились всего лишь на одном примере, формализованном в выражении (11), которое мы привели к виду (16). Простота этого выражения подкупает и позволяет сделать вывод, что субъективные оценки качества сведены к минимуму, а значит и ошибки.

Остановимся еще на одном аспекте наших оценок, мы имеем ввиду значение числа К*, т.е. мера требовательности и мера соответствия этим требованиям, то есть повышение и понижение значения К* (классическое понимание маркетологических исследований) — теперь мы можем это значение контролировать и анализировать.

Это связано с тем, что повышение или понижение значения К* приводит к несоответствию декларируемых целей и их конкретных результатов. Однако эти вопросы выходят за рамки настоящей публикации, но они также решены автором.

Итак, подведя итог наших рассуждений, мы смело можем утверждать, что нам удалось формализовать оценку качества, а также оценку деятельности и осуществлять непрерывное диагностирование любого процесса, где формально описаны связи (логика процесса). Автору настоящей статьи неизвестны другие теории, которые позволяют проводить подобные операции в непрерывнозначной постановке.

Список литературы

1. Голота Я.Я. Непрерывнозначная логика. РЖМ, 1983, №2, реф. А46-Деп. Рукопись депонирована в ВИНИТИ №5154-82 от 14.10.82г. 74с.
2. Чернышев А.В. Проектирование стендов для испытания и контроля бортовых систем летательных аппаратов: Учебник для авиационных специальностей ВУЗов. — М.: Машиностроение, 1983г, 384с.
3. Соколюк В.Н. и др. О численной характеристике состояния сложных технических систем. Сб.: Автоматизированные системы управления и средства автоматики в пищевой промышленности. Краснодарский политехнический ин-т., 1987, 128с.
4. Соколюк В.Н., Миронов В.В. Бизнес проектирование новое понятие для России. Информационный бюллетень Фонда Имущества г. Санкт-Петербурга №12, 1996г. 8с.
5. Гаркавенко С.И., Суганов В.И. О доопределении минимальной совокупности точек контроля с целью поиска неисправностей произвольной кратности в непрерывных объектах диагностирования. // Автоматика и телемеханика. №7. 1977г. 175с.
6. Голота Я.Я. О двух подходах к пониманию отрицания в непрерывнозначных логиках. Рукопись депонирована в ВИНИТИ №6464-82 от 29.12.82г.. 35с.
7. Голота Я.Я., Денисов А.А. Логика развивающаяся не вполне определенных систем. РЖМ 1986, №8, реф. 8А60ДЕП, ВИНИТИ №3002-13, от 20.04.86г. 74с.
8. Соколюк В.Н. и др. Оценка качества картографических шкал. // Известия ВУЗов, Геодезия и аэрофотосъемка. №4, ЛГУ, 1989г. С.38-42.
9. Соколюк В.Н. и др. Методика создания оценочных карт с использованием непрерывнозначной логики. // Рациональное использование природных ресурсов и охрана окружающей среды.— Л.: ЛПИ. 1988. Выпуск 11. С.97-103
10. EOQC Quality? 1981, 25, №4, с. 3-4.
11. Сиро С., Практическое руководство по управлению качеством. Пер. с четвертого японского издания С.И. Мышкиной, //под ред. В. И. Гостева., М., Машиностроение. 1980, с. 8.
12. Искусственный интеллект: ЭВМ заменяет рассуждения менеджеров. США.//Artificial intelligence — replacing managerial judgment with computer. Coats. P.J. Bull Forecast, 1986, 5, №1, с.12-14.
13. Азгальдов Г. Г. Теория и практика оценки качества товаров. — М.: Экономика. 1982. С.132.

Версия для печати  |  Пользовательское соглашение