Неопределенность, изменчивость и противоречивость в задачах качественного анализа
Соколюк В. Н.
Пояснительная записка
Теория формально определяет любую динамическую систему Σ как некоторый математический объект вида Σ:{ξ;φ;ζ},
представляющий совокупность множеств входов -ξ, выходов -φ и связывающих их системообразующих отношений -ζ. Такие наборы
взаимосвязанных множеств Σ⊂ξ×φ определяют только количественные проявления
системы, что является далеко недостаточным для анализа и оценки её целенаправленного функционирования. Для того чтобы математический результат мог быть содержательно воспринят, необходима его качественная непротиворечивая интерпретация.
Именно введение интерпретации дает возможность нам считать, что математические системы являются моделями реальных объектов. Для введения интерпретации математических моделей реальных или физически реализуемых объектов необходимо разработать соответствующую процедуру, отражающую целенаправленность
функционирования объекта, его физическую сущность, прагматику и восприятие.
Разработка такой процедуры интерпретации, учитывающей именно качественные особенности функционирования системы, не может основываться только на представлении ее свойств, локализованных в одной (математической) точке.
Для учета таких качественных свойств был предложен ряд методов, как нечеткие множества, пространства толерантности и пороги различимости. Все эти методы преследовали одну и ту же цель: дать количественную оценку накопления несущественных качественных различий, имеющих место в движении
(динамике) системы.
Поэтому представляется существенным для общей теории разработка метода или методики введения качественных различий и интерпретации проявляемых свойств динамических систем, так как оценки качественных различий и условия их интерпретации лежат в основе анализа целенаправленного функционирования
любой конкретной и реальной динамической системы. Если количественные характеристики системы в математической модели строго определены свойствами множества Х=ξ×φ и
отображением ζ., то методика представления ее качественных свойств пока ещё не разработана в широкой практике. А вместе с тем, именно выявление конкретных качественных проявлений системы позволяет дать корректное обоснование для ее применения, а также
сведения о ее физических свойствах. Поэтому всегда в конкретных исследованиях, хотя бы в неявном виде, возникает проблема найти тот максимум достоверной информации, который содержит математическая модель относительно свойств реального объекта.
По существу, это задача о количестве качественной информации, содержащейся в математической модели конкретного объекта.
Главное в этой задаче: качественная интерпретация количественных соотношений, составляющих математическую модель.
Для ее решения необходимо построить процедуру выделения в Х тех значений переменных х∈Х, которые характеризуют определенное качественное свойство реальной системы, отраженное в формальной системе ∑. Следовательно, такая
своеобразная дополнительность — задание количественных и качественных свойств — дает полное представление о реальной системе по ее модели с точки зрения конкретного наблюдения. Очевидно, для выделения качественных свойств системы надо все ее проявления, т.е. значения всех х, эквивалентных
с определенной точки зрения, объединить в одно множество, определяющее соответственное качественное условие ϑ.
Для того чтобы учитывать сколь угодно малое изменение качественной информации, автор настоящей статьи предлагает математический аппарат и метод, разработанный на основе нового понимания закона отрицания и названный метод ГЛАС® (Гибкая Логика Антонимических Систем)®. (Можно
ГЛАС® вопиющего в пустыне).
Сущность настоящего метода состоит в том, что истина и ложь, рассматриваемые в классической двузначной логике, предполагают исчерпывающие значения всех объектов изучения и всех обстоятельств, при которых они рассматриваются. Однако такие ситуации, когда людям известно все относительно
того, с чем они имеют дело, крайне редки. Можно с уверенностью говорить о том, что люди чрезвычайно редко располагают исчерпывающей информацией, “абсолютными” знаниями. Как правило, приходится действовать, принимать те или иные решения, делать соответствующие заключения, находясь в
условиях неполных знаний (неполной информации). В подавляющем большинстве случаев истинностный характер утверждений не может быть определен всего лишь двумя значениями: истина и ложь. В человеческих рассуждениях нет просто истинных и ложных утверждений, а есть истинные и ложные утверждения с разной степенью
истинности и ложности. Степень истинности весьма расплывчата, причем истинность одного и того же не во всех ситуациях одна и та же. Мы исходим из того, что в своих рассуждениях о реальном мире, в логических умозаключениях люди интуитивно пользуются не двумя, а неограниченно большим числом истинностных
значений. Истинностные значения, которые рассматриваются в двузначной логике, являются предельными для тех значений, которые в действительности используются в умозаключениях. То есть имеют место непрерывные значения оценочных показателей истинности или лжи. Таким образом, напрерывнозначная логика является
той моделью, которая как бы ближе к действительности (к человеческой логике различных "оттенков"), чем двузначная.
Оперируя относительными истинами, люди невольно прибегают к двузначной логике (округляя относительные истины до абсолютных) или используют теорию вероятностей (или что-нибудь связанное с понятием вероятности). Поэтому первым этапом реализации метода ГЛАС® стала теория, позволившая
объединить (без противоречий) двузначную логику, логику высказываний, теорию вероятностей.
Первые публикации относятся к 1982 году. В них дана формализованная оценка неопределенностей. Дальнейшее развитие метода дало возможность формализовать такое философское понятие как изменчивость. Далее авторы пытаются определить (формализовать) противоречивость. Таким образом, возникает
естественная посылка определить разрабатываемый метод ГЛАС® как аппарат диалектической логики, который учитывает такие понятия, как неопределенность, изменчивость, противоречивость. Однако необходимо признать, что до конца формализованы только два понятия — неточность и изменчивость. Формализация
противоречивости пока не получила своего красивого и не конфликтного с двузначной логикой завершения.
Не углубляясь в математическую сущность уже созданной теории и построенного на ее основе универсального метода ГЛАС®(о нем можно узнать по публикациям), авторы вкратце перечислят те практические приложения, которые удалось реализовать за весь период работ.
-
задача о назначениях I (групповая конкуренция)
- задача о назначениях II (индивидуальная конкуренция).
Все эти направления связаны с традиционными задачами кибернетики. Все они доведены до конкретных алгоритмов решения. В практической (технической, экономической) области авторам удалось найти алгоритмы решения задач, связанные с непрерывным диагностированием (мониторингом), а как следствие
с прогнозированием (исследуемого объекта) технического или экономического состояния той или иной динамической системы как в прямой, так и в обратной постановке. Авторам удалось значительно ускорить алгоритмы автоматизированного распознавания образов. Причем образы могут быть представлены как точками,
так и линиями и пятнами в очень разряженном виде.
Данная теория позволяет намного точнее определять (ранжировать, узнавать) необходимые действия операторов / управленцев, создавать структурные и системные связи и потом в узлах, проставляя решающие алгоритмы, создавать перестраиваемые или быстро перенастраиваемые системы,
а точнее сказать настраивающиеся системы на любые внешние и внутренние изменения, если изменяющиеся параметры / системы имеют логическую связь. Это является важнейшим параметром при принятии решений в супердинамичных системах. В таблицах ниже мы покажем это наглядно в представленных математических
выражениях. Чтобы понять основы теории ГЛАС®, и что за математический аппарат применен, нужно рассмотреть таблицу №2, где представлены основные этапы развития базовых логик.
Таблица №1.
Сравнительный анализ теории нечетких множеств и логики антонимов
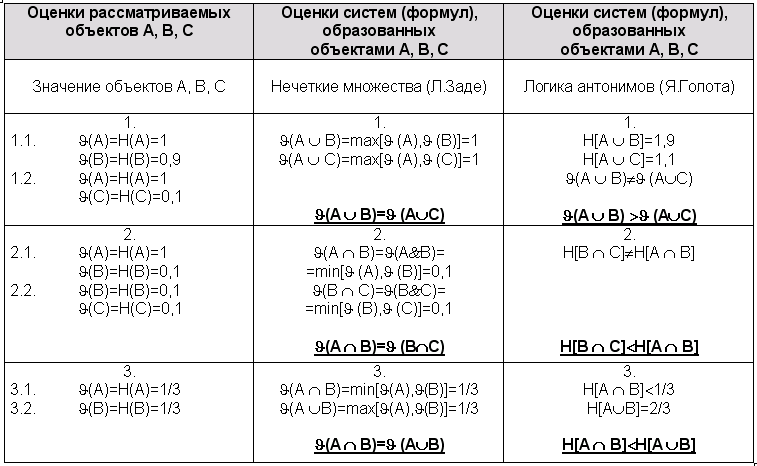
С сутью методологии и метода (теории) ГЛАС® можно будет ознакомиться в статье про раннюю диагностику, где будет показано и доказано, почему так необходимы более точные оценки, точное ранжирование (все это осуществляется
на примере уже известных оценок или информации с датчиков).
Таким образом, логика антонимов (ЛА) позволяет различать и по-разному оценивать те случаи, которые не различимы самыми новейшими традиционными методами.
Смело можно сказать, что ЛА является более чувствительным (тонким) инструментом, чем существующие на сегодняшний день традиционные методы.
Пример 3 показывает, что ЛА всегда отличит последовательную и параллельную связь, а традиционные теории могут и не отличить (различить).
Очевидно, что более тонкое ранжирование никогда не является лишним, особенно если дело касается человеческого фактора или весьма быстро протекающего процесса...
Основы представленной здесь теории (методологии) и практические технологические / технические методы были разработаны на основе теоретических разработок Я.Я. Голоты, проводившиеся в 1980-84 годах. Его теоретические разработки называются «Логика антонимов». Авторами данной
теории запатентованы алгоритмы (базовые формулы) и устройства, реализующие данные алгоритмы.
Таблица №2.
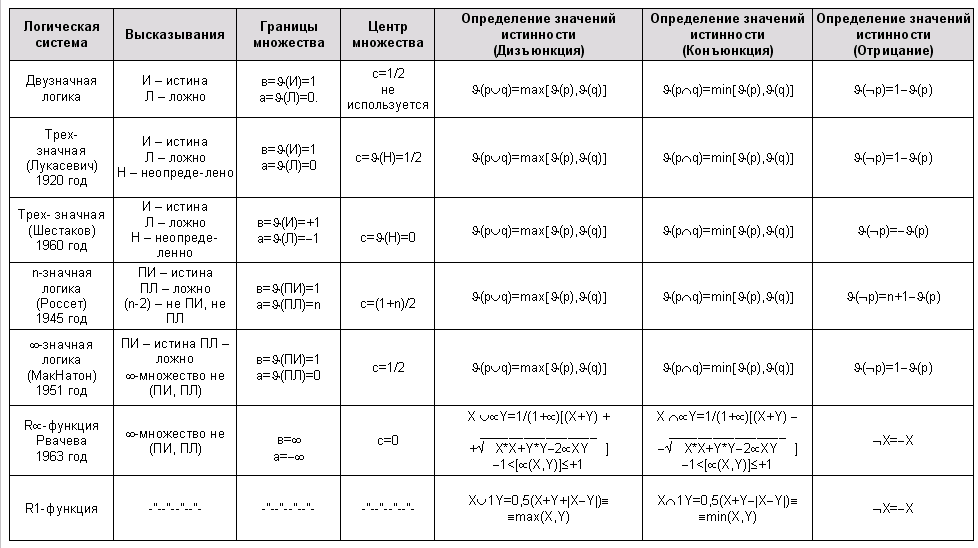
Сравнительный анализ всех существующих логик
Примечание
Под динамической системой мы понимаем систему с быстро изменяющимися во времени параметрами, причем зачастую формальные параметры системы нечетки — ”плохо” определены, изменчивы и противоречивы, например социальные
системы, экономические системы, правовые системы.
|